Par Plouf, mais si mais si…

Et plonk, voilà un tut qui va en faire fuir plus d’un : ça va être un truc 100% maths…

Tout ça grâce à un bête truc génial qui s’appelle la transformée de Fourier. Alors soyons clairs dès le début, je ne vais pas vous filer d’algorithmes qui font cette transformée, parce qu’ils sont abominables et qu’un copier/coller fera fort bien l’affaire. Moi ici je vais essayer de vous expliquer de quoi il en retourne, comme ça au moins vous saurez où chercher le jour où vous en aurez besoin.

Alors un signal temporel (ou assimilé), c’est une fonction du temps. Ca vous dit, pour un moment donné, quel est la valeur du signal. Alors un signal c’est quoi ? C’est une bête valeur, voilà tout (on appelle ça un signal, parce que c’est plus joli). La fonction y=sin(x) c’est un signal sinusoïdal, la valeur du signal c’est y, et le " temps " ici c’est x.

Vous savez (enfin, on espère) qu’un son, pour l’oreille, c’est une variation de pression de l’air sur vos tympans, qui est propagée (une onde, quoi…) depuis un haut-parleur qui a généré la même variation de pression quelques instants auparavant. Cette variation de pression est réalisée grâce à la membrane du speaker, qui avance (qui " presse l’air ") ou qui recule (" qui pompe l’air "), ce qui crée une augmentation ou une diminution de pression. On se rappellera que l’oreille n’est pas sensible à la pression (pour les sons du moins), mais uniquement à des variations de cette pression.

En général, on dit au speaker quelle doit être la position de la membrane au moyen d’un signal électrique (plus fort=plus loin, moins fort=moins loin, par exemple), lui-même amplifié par un ampli, le signal initial ayant été créé par notre cher ordinateur. Et lui, l’ordi, on lui a dit quelle était la valeur du signal en lui envoyant un octet ou une paire d’octet. Par exemple, en 8bit, 0 pourrait vouloir dire " a fond en arrière " et 255 " a fond en avant " pour la membrane du speaker.

Revenons à notre oreille. Plus la variation de pression est rapide, plus notre oreille entend un son aigu (et inversement). On dit qu’un signal est pur s’il correspond exactement à un signal de type sinusoïdal. Bref, si on dit au speaker de jouer un signal position=sin(t), avec t exprimé comme un nombre de secondes, on va avoir un son pur (dans les limites du speaker) qui sera joué à une certaine fréquence.

Alors la fréquence késako ? C’est le nombre de fois qu’on "boucle un tour du sinus " par seconde. Bref, le nombre de fois que le sinus vaut "1 " par seconde. Comme sinus vaut 1 en Pi, 3Pi, 5Pi, …, chaque fois que t vaudra une de ces valeurs, on aura fait un tour. Comme chaque valeur est distante de 2Pi, le nombre de tours par seconde vaudra 1/2Pi. C’est notre fréquence. Si notre signal c’est position=sin(440*2Pi*t), on aura un son de 440 hertz (1 hertz, ou 1Hz, signifie "une fois par seconde "), c’est le son du diapason.

Evidement, il est rare que l’on ait envie de jouer un son pur, et les vrais sons ressemblent fort peu à un sinus… Par contre, vous comprenez que si on veut mettre un son de 440Hz dans un fichier, c’est un peu bête de stocker tout le signal, il suffit de dire "ceci est un son de 440Hz " à la place, ce qui est franchement plus court. Ca a l’air con dit comme ça, mais je peux vous dire que si vous comprenez ça, vous avez compris une première bonne partie du codage MP3…

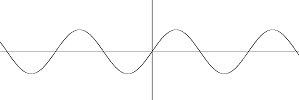
Attention, on rigole, à partir d’ici je vais vous demander de me croire sur parole.

Ceci est un bête sinus, comme ça je vous rappelle en même temps à quoi ça ressemble J

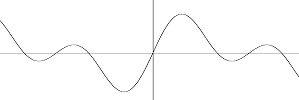
Je vais faire la somme d’un sinus et d’un sinus de fréquence diminuée de moitié.

Toujours rien de bien extraordinaire, mais ça ressemble tout de suite moins à un sinus. Si je voulais transmettre ce signal, je dirais "ceci est une somme de sinus, le premier est à 440Hz (par exemple), le second est à 220Hz ".

Je peux additionner plein de sinus, et je ne suis même pas obligé de prendre le même "poids " pour chacun des sinus. Ce que je veux dire, c’est qu’ici c’est sin(440*2Pi*t)+sin(220*2Pi*t), mais on aurait pu tout aussi bien prendre 5sin(440*2Pi*t)+17sin(220*2Pi*t). Ca aurait fait un autre petit dessin, et j’aurais dit "ceci est la somme d’un sinus de fréquence 440Hz et de poids 5, avec un sinus de fréquence 220Hz et de poids 17 ".

Plus je veux faire un truc compliqué, et plus je dois fournir d’information de ce genre, c’est logique…

Là où arrive le truc amusant de l’histoire, c’est que (on s’accroche) "tout signal peut se représenter comme une somme de sinus ". C’est à dire que je peux prendre n’importe quelle fonction, et la remplacer par une somme de sinus. Au lieu de transmettre le signal audio, je le transmets sous la forme suivante : " un sinus de 57Hz de poids 17, un autre de 36Hz de poids 72, un de 487Hz et de poids 12, … ". Je vous jure que je vais pouvoir avoir un signal aussi précis que je veux, pour autant que je prenne assez de sinus.

Alors jusque là, ya pas de miracles : en pratique, nous, on a (par exemple) un signal de 4096 échantillons (8 ou 16bits par échantillon), il va nous falloir 4096 informations de "poids " pour représenter le même signal (les fréquences ne doivent pas être transmises, on fixe à l’avance quelles fréquences on va utiliser pour représenter le signal, on peut, sisi, mais je me lance pas dans des détails techniques, on s’en fout ici). (Word me fait savoir que j’ai utilisé beaucoup de fois "on " dans cette phrase J )

Le principe de "décomposition d’un signal temporel en une série d’informations fréquencielles " s’appelle la "décomposition en série de Fourier ", alias la transformée de Fourier (c’est pas exactement la même chose, mais on s’en fout…).

L’algorithme qui nous permet, nous, avec des ordinateurs, de décomposer un signal discret en une suite discrète de fréquence est appelé la DCT : " discrete cosine transform ". Alors on utilise des cosinus et pas des sinus, mais ça revient exactement au même. Il existe même un algorithme très efficace pour faire de la DCT, c’est la FFT : " fast fourier transform ", c’est cet algorithme là que vous utiliserez sans doute si vous voulez faire un analyseur de spectre. Pis l’algo est efficace dans le sens où il est également capable de reconstituer un signal temporel à partir d’une série de fréquences. Evidement ça vous auriez pu le faire tout seul en faisant une bête somme de sinus, mais ça n’est pas très efficace comme méthode.

Tiens, tant qu’on en parle, du spectre…

Alors au vu de tout ce qui précède, ce qu’est un analyseur de spectre doit sauter aux yeux : c’est la représentation graphique de la décomposition en série de sinus : les premières bandes (les basses) représentent les poids des fréquences basses. Plus les poids des fréquences basses sont importants, et plus on les entend (c’est logique), et plus on dit qu’ "il y a des basses ". Même chose pour les aigus. En réalité, si le speaker est bon, ainsi que l’analyseur, si je joue un son "pur " sur un ampli, l’analyseur doit afficher zéro partout, avec juste une pique sur la fréquence jouée.

Par exemple, sur un analyseur, mon premier sinus devrait apparaître comme ceci :

Et mon bidule du second exemple, comme ceci :

Mon exemple avec 5 et 17 donnerait à peu près ceci (qualitativement) :

Evidement, si le wav fait 50mo, ça va faire un peu lourd, c’est pourquoi on fait ça par petits morceaux : on décompose un paquet de 4096 échantillons, on repondère, on recompose, on joue, on prend les 4096 échantillons suivants, on les décompose, etc… C’est mathématiquement moins précis que de le faire sur tout le signal d’un coup, mais c’est plus "réalisable ".

Un filtre, c’est une sorte d’égaliseur brutal : un filtre passe-bas, c’est un filtre qui "oublie " toutes les fréquences au-dessus d’une certaine valeur limite. Par exemple, au-delà de 20kHz, l’oreille est dépassée, on arrive dans les ultra sons, donc inutile de les jouer. Il est également souvent inutile de jouer des fréquences au-dessus de 10Khz, parce qu’une musique arrive rarement aussi haut. A cette fréquence, c’est le "bruit de fond " qui s’y trouve, c’est pour ça qu’on filtre ces fréquences trop hautes et souvent inutiles.

On peut, de la même façon, faire un filtre passe-haut qui "oublie " les fréquences trop basses, mais c’est plus rare, parce que nous, les basses, on aime ça J

Mais on peut comprendre l’utilité d’oublier des gammes de fréquences : souvent ça laisse le son compréhensible, et… il ne faut plus les transmettre, bien sûr ! On peut ainsi facilement oublier la moitié des fréquences et encore comprendre ce que dit une personne. Voilà comment fait le téléphone…

On vient de trouver une première façon de compresser un signal audio. Le problème avec cette méthode, c’est que même si les voix restent audibles, la qualité s’en ressent tout de même beaucoup (Vous imaginez votre mp3 en "qualité téléphone ? "). Alors l’idée, c’est d’y aller plus "soft ", et plus intelligemment. Ce système s’appelle la quantification des poids des fréquences. En pratique, ça revient à "réserver moins d’information (de bits) pour des poids de fréquences moins importantes ".

Je m’explique : comment sont stockés les poids des fréquences en mémoire ou sur le disque ? Ben, dans des entiers ou des nombres en virgule flottante (en réalité, ça revient au même, mais si mais si, et donc on va se contenter du cas où elles sont dans des entiers). Imaginons que le résultat du calcul de la DCT pour une fréquence donnée tient sur 16bits, donc des valeurs de 0 à 65535.

Ben si cette fréquence est peu importante, je vais approximer son poids "à la grosse louche ", c’est à dire en ne lui donnant plus que, mettons, 4bits. Au lieu d’aller chercher des valeurs entre 0 et 65535, il ira les chercher entre 0 et 15. Evidement, je dois me souvenir que je dois remultiplier cette nouvelle valeur par 4096 pour retrouver la valeur originale, mais, au final, je n’ai plus qu’à transférer 4bits au lieu de 16. Evidement, la valeur est moins précise, mais croyez-vous vraiment que votre oreille fait la différence entre un poids de 4096 et un autre de 4098 vers 5kHz ? La réponse est non…

Par exemple, si je sais que l’oreille n’entend pas très bien les fréquences dans les environs de 4kHz, je vais approximer, à cette fréquence, un poids de 8289 par 8192 (=2*4096). Donc je vais transmettre 0010 au lieu de 10000001100001. Le décodeur sait, lui aussi, que j’ai stocké ces valeurs sur 4 bits, qu’il doit donc multiplier par 4096, et jouera un son de 4kHz avec un poids de 8192 à la place de 8289. Vous n’entendrez pas (ou si peu) la différence.

Evidement, pour un son dans les environs de 500hz, on ne peut plus se permettre une telle approximation, et on stockera son poids sur, mettons, 12bits. (L’oreille est plus attentive à cette gamme de fréquences)

Et le résultat de ce codage ? Ben c’est une suite de 1 et de 0, beaucoup plus courte que l’originale, qu’il reste à "zipper ", c’est à dire à compresser avec un bête codage de Huffman ou du même style, car ça nous fera encore gagner quelques octets… Le résultat, vous le connaissez : Un facteur 10 de compression pour une distorsion inaudible pour notre oreille.

Alors tout ce qu’on vient de dire, ça marche pour un signal temporel. Mais bon, remarquez que ça peut bien marcher pour n’importe quel autre signal, après tout, ce que l’algo de la FFT "voit ", c’est une suite d’octets les uns à la suite des autres. Donc on peut compresser n’importe quelle suite d’octets avec cette méthode, pour autant qu’on soit d’accord d’avoir un résultat un rien dégradé par rapport à l’original.

Et pouet, vous avez (du moins en principe) un jpeg. Et plus vous voulez de qualité, et plus vous allez être précis dans vos fréquences. Si vous n’être pas précis, c’est à dire si vous n’autorisez presque pas de bits pour les poids des fréquences hautes, vous allez perdre des détails (vu que les fréquences hautes, ce sont justement celles qui correspondent à des variations brusques de l’image, et donc les détails ou les frontières nettes). Vous allez donc avoir cet espèce de "flou " caractéristique du codage d’image. Avec un très grand taux de compression, vous pouvez très bien observer les blocs séparés, car à force de les simplifier, ils finissent par ne plus "coller " entre eux, nos pauvres blocs…

Il existe également des décompositions de Fourier en vraie 2D, et il y a une infinité de variations sur le thème, en fonction de la nature de l’image à compression, si c’est une vidéo, etc… Mais c’est toujours le même principe de base.

Tout ce que je viens de dire est un méga résumé, absolument pas rigoureux, hyper simplifié, mais les concepts et les principes s’y trouvent. Evidement, mettre tout ça en musique dans un soft qui tourne, c’est autre chose. Mais il faut toujours se souvenir de ce qu’il y a "derrière ", et ici, c’est relativement simple, au fond, si on a bien pigé que tout signal peut se représenter comme une somme pondérée de sinus.